
上篇文章介绍了如何使用 Backetsting.py 快速上手。今天继续介绍另一个策略回测时非常重要的点,参数优化。参数优化是提升策略表现的重要步骤,而 Backtesting.py 内置了参数优化功能,使用起来还是很方便的。
本文将用上篇的案例 SMACrossStrategy 策略演示 Backtesting.py 参数优化。
优化示例
Backtesting.py 默认优化方式是将是将所有的参数组合穷举遍历一遍,这种方式也被称为-网格搜索。
以下是优化 SMACross 策略的示例代码:
1
2
3
4
5
6
7
| bt = Backtest(GOOG, SMACrossStrategy, cash=10000, commission=0.002)
stats = bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
)
print(stats)
bt.plot()
|
通过 range 指定了 fast_ma_window 和 slow_ma_window 的参数范围,运行的结果就是表现最好的参数的结果。
通过 stats._strategy 拿到策略实例,然后打印策略实例参数。
1
2
3
| print(stats._strategy)
print("fast_ma_window", stats._strategy.fast_ma_window)
print("slow_ma_window", stats._strategy.slow_ma_window)
|
输出:
1
2
3
| SMACrossStrategy(fast_ma_window=5,slow_ma_window=20)
fast_ma_window 5
slow_ma_window 20
|
网格搜索适用于参数空间较小的情况,超参数的场景还要考虑其他优化方法。先暂时只介绍这个默认的优化方法。
参数约束
上面的优化代码有个明显的不合理,可能出现 fast_ma_window 大于 slow_ma_window 的情况,如 fast_ma_window=20,但 slow_ma_window=10 的组合,这不仅会增加优化耗时,也不符合策略的逻辑,。backtestingpy 的优化器提供了参数约束能力,我们可以限制 fast_ma_window 必须小于 slow_ma_window。
示例代码:
1
2
3
4
5
| stats = bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
)
|
通过 constraint 指定参数约束函数,限制 fast_ma_window 必须小于 slow_ma_window。这能极大提升回测优化速度。
优化标准
优化器默认只返回了一个表现最好的那个参数组合,但这个最好是如何评价的呢?
Backtesting.py 优化器的默认优化标准是 SQN,它的计算公式如下:
1
| SQN = (平均每笔交易收益 × √交易次数) / 每笔交易收益的标准差
|
一句话表述它的含义就是,SQN 通过平均收益(高更好)、收益波动性(低更好)和交易次数(多更好)衡量策略稳健性,值越高越优质。
我想修改这个标准可以吗?当然可以。
optimize 提供了一个名为 maximize参数来修改优化标准。我可以将最大回撤或夏普比率作为优化标准。
将优化标准改为最大回撤:
1
2
3
4
5
6
| bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
maximize='Max. Drawdown [%]',
)
|
将优化标准改为夏普比率:
1
2
3
4
5
6
| bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
maximize="Sharpe Ratio",
)
|
优化函数
这个优化标准默认是选设置的优化指标的最大值,如果想越小越好,可将传递优化指标名改为函数,自定义标准。
如选择年化波动率最小的参数组合,示例代码:
1
2
3
4
5
6
| bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
maximize=lambda r: -r["Volatility (Ann.) [%]"],
)
|
通过匿名函数 maximize=lambda r: -r["Volatility (Ann.) [%]"] 选择年化波动波动率最小的组合。
不过,从我平时的使用体验来看,还是默认的 SQN 的优化结果比较合理,它的评价维度更加全面。
自定义优化指标
除了那些内置的优化指标,我还可以自定义标准。举个例子,我现在想寻找 “在市场中持仓时间最短收益最大” 的参数组合。
定义优化目标函数:
1
2
3
4
| def equity_per_exposure(r):
final_equity = r['Equity Final [$]'] # 最终净值
exposure_time = r['Exposure Time [%]'] # 持仓时间
return final_equity / exposure_time
|
目标函数是通过最终净值除以持仓时间比率计算得到,将其传递给 bt.optimize。
注:如要准确计算 “持仓时间” 要用 持仓时间占比 * 总时间,这省略了,因为它不影响策略的评估结果。
1
2
3
4
5
6
| stats = bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window.
maximize=equity_per_exposure,
)
|
如果用这个指标优化策略,得到的参数组合可能交易次数很少,因为这样容易出现持有时间短,收益高的情况。这不是我想要的。
如何解决这个问题?
还可以在优化函数中添加条件约束,确保得到参数组合是的合性。在函数中加上如果交易次数小于 50 次,返回 -1,保证它们不会被优化结果选中。
1
2
3
4
5
6
7
| def equity_per_exposure(series):
if series['# Trades'] < 50:
return -1 # 返回负值以避免选择
final_equity = series['Equity Final [$]']
exposure_time = series['Exposure Time [%]']
return final_equity / exposure_time
|
好像通过交易次数约束不太合理,那还可以基于单位时间交易次数过滤,如交易频率 100 天要至少交易 1 次。
1
2
3
4
5
6
7
| def equity_per_exposure(series):
if r["# Trades"] / r["Duration"].days < 0.01:
return -1
final_equity = series['Equity Final [$]']
exposure_time = series['Exposure Time [%]']
return final_equity / exposure_time
|
通过自定义优化指标,可以更灵活地定义你的目标,发现满足你需求的最佳参数组合。
参数优化热力图
参数优化热力图是一种直观的方式来比较不同参数组合对策略表现的影响。通过可视化参数范围内的结果,可以快速识别最佳参数区域。
Backtesting.py 中支持生成热力图的方法。
生成基础热力图
在优化函数 optimize 中要启用热力图选项 return_heatmap。
1
2
3
4
5
6
| stats, hm = bt.optimize(
fast_ma_window=range(5, 50, 5),
slow_ma_window=range(10, 100, 10),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
return_heatmap=True
)
|
优化函数 bt.optimize 返回了两个对象,其中的第二个对象是 hm 就是绘制热力图的数据,包含了所有参数组合的优化结果。
打印下 hm 变量。
输出:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| fast_ma_window slow_ma_window
5 10 1.792704
20 2.703298
30 2.392251
40 2.257054
50 1.794700
10 20 2.643361
30 1.938471
40 2.427356
50 1.603184
15 20 1.832693
30 1.720452
40 1.762611
50 1.365671
20 30 1.316673
40 2.230364
50 1.389500
25 30 1.178816
40 2.128967
50 0.915063
Name: SQN, dtype: float64
|
参数组合对应的值就是优化指标的值,因为我的 optimize 没有指定 maximize,默认值就是 SQN。
有了数据后,就可以用 Backtesting.py 内置函数 plot_heatmaps 绘制热力图了。
1
| from backtesting.lib import plot_heatmaps
|
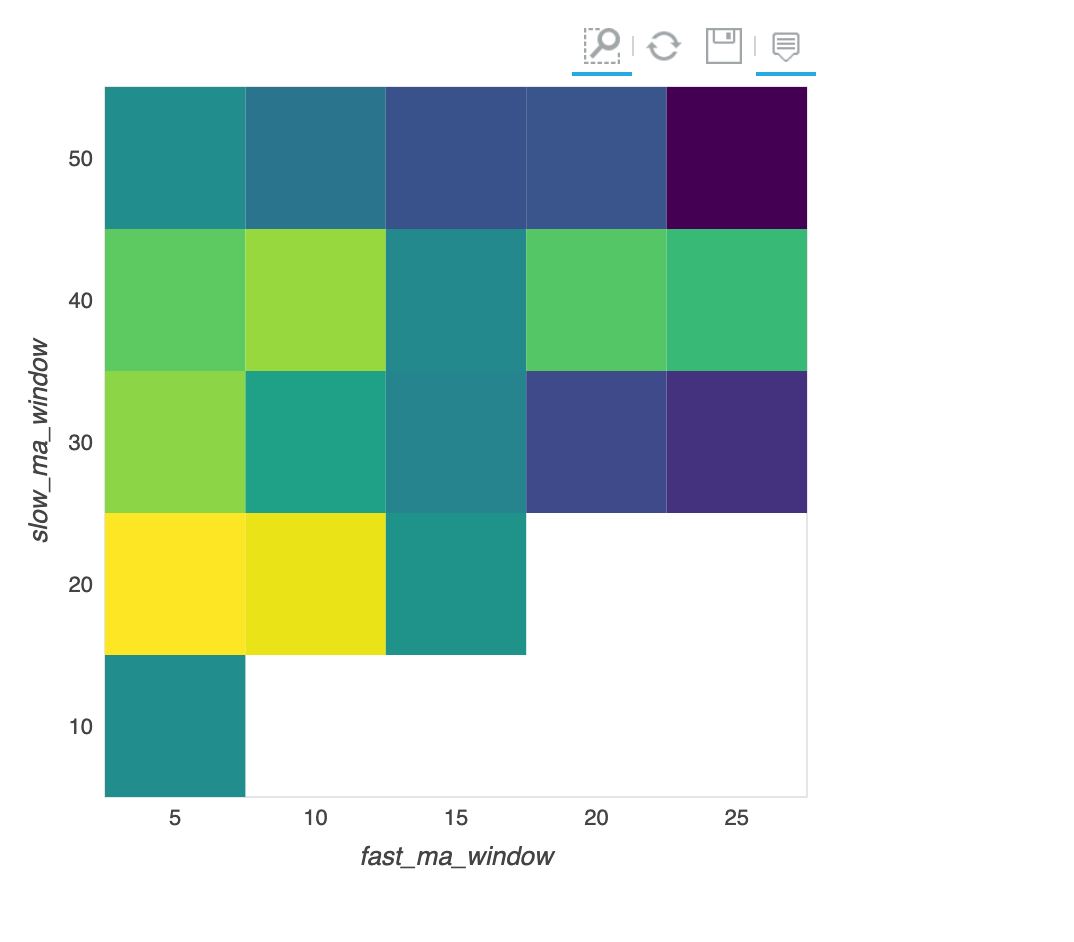
粗略查看,表现最好区域在黄色区域,大概是 fast_ma_window 位于 [5, 10], slow_ma_window 位于 [20, 30, 40] 区域;
多参数组合的热力图
现在的 SMACrossStrategy 策略只有两个参数,如果是三个或更多参数,plot_heatmaps 会将参数两两组合绘制每个组合的热力图。
简单修改下 SMACrossStrategy 的逻辑,加上 ATR 止损,通过一个 atr_factor 控制止损的乘数,如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class SMACrossStrategy(Strategy):
# 参数
fast_ma_window = 10
slow_ma_window = 20
atr_factor = 3
def init(self):
self.fast_ma = self.I(
talib.SMA, self.data.Close, timeperiod=self.fast_ma_window
)
self.slow_ma = self.I(
talib.SMA, self.data.Close, timeperiod=self.slow_ma_window
)
self.atr = self.I(
talib.ATR, self.data.High, self.data.Low, self.data.Close, timeperiod=14
)
def next(self):
if self.fast_ma[-1] > self.slow_ma[-1] and not self.position:
self.buy(sl=self.data.Close[-1] - self.atr_factor * self.atr[-1])
elif self.fast_ma[-1] < self.slow_ma[-1] and self.position.is_long:
self.position.close()
|
同时参数优化加上 atr_factor:
1
2
3
4
5
6
7
| stats, hm = bt.optimize(
fast_ma_window=range(5, 30, 5),
slow_ma_window=range(10, 60, 10),
atr_factor=range(1, 4),
constraint=lambda p: p.fast_ma_window < p.slow_ma_window,
return_heatmap=True,
)
|
将新得到的 hm 交给 plot_heatmaps 绘制。
1
| plot_heatmaps(hm, agg='mean')
|
其中有个 agg 参数,它指定了分组聚合方式,默认为 max,这里修改为 mean,即采用平均值聚合。
新生成的热力图:
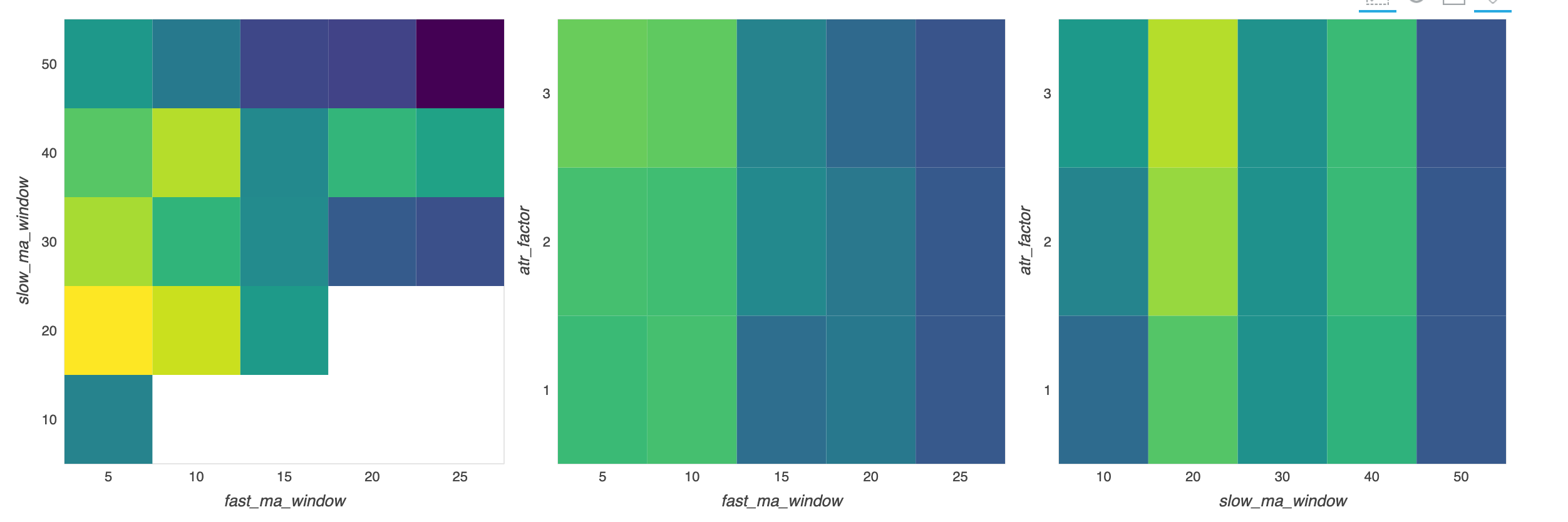
如果参数过多,组合数量会急剧增加,且大部分的组合(如 atr_factor 和 fast_ma_window)没有分析价值,我们可以通过 pandas 分组聚合提取想要的参数组合。
示例代码:
1
2
| hm = hm.groupby(by=["fast_ma_window", "slow_ma_window"]).mean()
plot_heatmaps(hm)
|
注意点
- 热力图适用于分析两个参数间的关系,如果参数过多,图表数量会急剧增加。
- 使用合理的参数范围和步长可以减少计算量并提高可读性。
- 更灵活的使用方法,可分组聚合关心的参数组合进行分析。
通过查看参数优化热力图,可以高效地探索参数空间,不仅能找到表现最佳的策略组合,还能减少选出过拟合参数组合的可能性。
总结
本文介绍了如何在 Backtesting.py 中进行参数优化,包括基础的网格搜索、参数约束、自定义优化指标以及通过热力图可视化优化结果等内容。通过这些方法,可以有效提升策略的表现,同时避免无意义的参数组合。热力图为分析参数间的关系提供了直观工具,是优化策略的重要辅助。掌握这些技巧,可以更高效地开发和改进交易策略。
希望本文对你所有帮助。



